Hoy os propongo un juego un tanto más dificil:
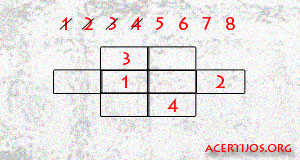
Nuestro objetivo consiste en situar todos los números que aparecen arriba, es decir, del 1 al 8, en cada uno de los recuadros del casillero, con la condición de que números correlativos no pueden tocarse, ni lado a lado ni en diagonal. En el ejemplo, los números del 1 al 4 están correctamente situados, y aún se puede seguir… ¿hasta el final?
Obviamente, podeis empezar a situar los números como mejor os plaza, este sólo es un ejemplo gráfico para que comprendáis la finalidad del juego.
Os propongo dos alternativas:
- ¿Eres capaz de situar todos los números del 1 al 8 en la rejilla sin que los números correlativos se toquen pero permitiendo que el 1 y el 8 estén juntos?
- ¿Y eres capaz de hacerlo sin que se toquen el 1 y el 8?
¡Espero vuestras respuestas! 😉 ¡Buena suerte!
Pues deduciendo
1)Los 2 del centro se tocan con 6 casilleros cada uno. Sólo el 1 y el 8 tienen 1 sólo vecino por lo tanto esos dos casilleros son para ellos.luego el 7 va al lado del 1 y el 2 al lado del ocho
el medio queda
7 1 8 2
el 3 debe ir en diagonal al 7 y el 6 en diagonal al 2, además uno arriba y otro abajo pues si no el 4 y 5 sse tocarían, luego el 5 al lado del 3 y el 4 al lado del 6.Listo
4 6
7 1 8 2
3 5
Impresionante. De verdad. Yo también sé hacerlo pero me llevó bastantes intentos…
¿Has probado a hacerlo impidiendo que el 1 y el 8 estén en las casillas centrales? es decir, ¿que «no se puedan tocar», como el resto? 😉
A ver qué se te ocurre 🙂
He conseguido hacerlo con el 1 y el 8 tocándose pero creo que es imposible hacerlo sin que se toquen. A primera vista no lo consigo.
Saludos!
Muy bien por tu esfuerzo. Que yo sepa nadie ha conseguido resolverlo si se tocan el 1 y el 8… es de aquellos ejercicios de lógica geométrica que parecen posibles pero, probablemente son imposibles 🙂
¡Enhorabuena!
buenas…
de partida no dare solucion a la primera porque ai multiples soluciones para la misma
eso si… estoy casi 100% seguro q es imposible realizarlo sin que el 1 y el 8 se token… la explicacion… es un poko dificil solo decirla… necesitaria el dibujito i todo xD pero doi el voto a q es imposible xD
En principio es imposible, aunque no he podido comprobarlo ni conozco las fórmulas matemáticas que demuestren que es imposible realizarlo de esta forma. Pero vamos, en la práctica, lo que ya dije, no conozco a nadie que haya conseguido resolverlo 🙂
qu facil es esa guea de mierda lo resolvi en un abrir y serar de ojo esto me demore:
1 año xDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDD